本文继续上一篇文章(大语言模型入门:从训练到推理)介绍一下 LoRA 微调的实现过程与原理,大语言模型由于参数量巨大,如果使用传统的全参数微调,需要大量的 GPU 资源且耗费很长时间,LoRA 微调就是为了解决这类问题, 可以通过 LoRA 微调让一个大语言模型更好的回答特定领域(eg. 医疗)的相关问题,LoRA 是一种参数高效微调(Parameter-Efficient Fine-Tuning, PEFT)方法,旨在通过低秩分解的方式对预训练模型进行微调。 相比于全参数微调(Full Fine-Tuning),LoRA 只需要更新少量的参数。 LoRA 的核心思想是:在模型的权重矩阵中引入低秩分解,仅对低秩部分进行更新,而保持原始预训练权重不变,并且还支持与原始权重合并,最终模型和原始模型参数量一致,不会增加推理耗时。
还是以开源项目 MiniMind 作为例子,这里下载了开源作者提供的 lora_medical.jsonl 作为训练集,训练集内容如下,结构与上一篇文章中提到的 sft 完全一致:
{"conversations": [{"role": "user", "content": "丘脑下部闭经的治疗方法"}, {"role": "assistant", "content": "丘脑下部闭经,也被称为功能性闭经,是由于丘脑下部-垂体-卵巢轴的功能失调导致的。..."}]}
{"conversations": [{"role": "user", "content": "甲亢是由什么引起的?"}, {"role": "assistant", "content": "甲状腺功能亢进症,通常被称为甲亢,是由于各种原因导致的甲状腺激素分泌过多的病症。..."}]}
使用以上的训练集进行 LoRA 微调训练,可以让 LLM 回答医疗相关的私有领域知识,这个知识在预训练知识之外;预训练代码位于 train_lora.py, 由于代码默认是以强化训练后的模型作为基座模型训练的,所以需要看情况修改一下 init_model:
def init_model(lm_config):
tokenizer = AutoTokenizer.from_pretrained('./model/minimind_tokenizer')
model = MiniMindLM(lm_config)
moe_path = '_moe' if lm_config.use_moe else ''
ckp = f'./out/full_sft_{lm_config.dim}{moe_path}.pth' # 视情况修改一下加载的基座模型
state_dict = torch.load(ckp, map_location=args.device)
model.load_state_dict(state_dict, strict=False)
return model.to(args.device), tokenizer
然后再指定一下 --data_path 和 --lora_name 用于加载训练集和输出模型名称就可以启动微调训练了:
LLM 总参数量: 26092032
LoRA 参数量: 262144
LoRA 参数占比: 1.00%
Epoch:[1/50](0/1580) loss:1.922 lr:0.000055000000 epoch_Time:141.0min:
Epoch:[1/50](100/1580) loss:1.871 lr:0.000054999802 epoch_Time:4.0min:
Epoch:[1/50](200/1580) loss:1.838 lr:0.000054999209 epoch_Time:3.0min:
...
Epoch:[50/50](1300/1580) loss:1.449 lr:0.000005001550 epoch_Time:0.0min:
Epoch:[50/50](1400/1580) loss:1.606 lr:0.000005000640 epoch_Time:0.0min:
Epoch:[50/50](1500/1580) loss:1.532 lr:0.000005000127 epoch_Time:0.0min:
可以看出 LoRA 微调的参数量只占了原模型参数总量的 1.00%,所以每个 Epoch 所需的耗时就大幅度减少了,几分钟就能完成一轮训练,为了达到更好的效果默认参数下需要训练 50 轮, loss 从 1.9 降到 1.5 左右,训练完成之后就可以试一下效果了。分别使用上一篇文章最后 sft 训练的模型和使用医疗领域知识 LoRA 训练的模型做对比:
| 问题 | SFT 模型 | LoRA 模型 |
|---|---|---|
| 我最近经常感到头晕,可能是什么原因? | 可能有一些感觉或情绪不佳或情绪问题,比如睡眠不足、饮食不当、过度使用电子设备等等。您可以尝试进行一些调整,比如运动、放松、睡眠等方式来缓解头晕。 | 头晕可能是由于以下几种原因:手部疲劳:手部的疲劳感也可能导致头晕。这是由于长期的高血压,如高血压,导致血糖水平升高。注意力不集中:手部的疲劳感可能会导致注意力不集中,从而出现头晕。这是由于注意力不集中,导致的头晕。饮食不均衡:过度饮食可能会导致头晕。这可能会影响睡眠,影响睡眠。偏头痛:过度的饮食可能会导致头晕。这可能会导致头晕。情绪波动:情绪波动可能会影响睡眠,导致头晕。压力或压力水平过高:压力过高可能会导致头晕。这可能会导致头晕。如果你的头晕持续不减或者伴随其他症状,建议你去医院进行检查。医生可能会建议你进行一些检查,如血液检查,以确定头晕的具体原因。如果是由于压力引起的,医生可能会建议你做一些改变来缓解头晕。 |
| 肺部有节结怎么办? | 肺部的节结一般是这样的:首先,你可以在肺部周围喝一杯水,然后将血液注入体内,再通过肺泡将气体吸收。接下来,将食物中的某些部分(如叶子、茎、花卉)缓缓地添加到膜内,以防止进一步扩张。 | 肺部有节结(CBT)和结节(结节结合)可能是由于肺部疾病、肺炎、肺部感染或肺癌引起的。这两种疾病是严重的并发症,需要立即治疗。肺部感染:这是一种严重的肺部疾病,需要立即的医疗干预。大多数肺部感染是最常见的病症,如果不及时治疗,可能会导致感染和严重的肺部感染。结节结节结节结节结节结:如果结节结是由于肺炎引起的,可能需要手术切除。如果结节是由于肺炎引起的,可能需要使用抗生素和抗生素。肺癌:这是一种由肺炎引起的肺癌,通常由癌细胞引起,症状包括:疲劳、肩膀或脚踝感染、呼吸困难、乏力、头痛、视力下降等。如果出现上述症状,应立即就医。请记住,这些只是可能的原因和治疗方法,具体的治疗方案应由您的医生根据您的具体情况来决定。请务必与您的医生密切沟通,了解您的病情和治疗方案。 |
| 发烧可能是什么原因? | 目前为止,是因为对抗抗病毒,而人类的健康状况和进食行为导致的。 | 病毒感染:虽然有可能出现病毒感染,但感染的可能性相对较小。感染的可能性取决于感染的严重程度,可能包括感染的程度。感染:感染可能会引起其他并发症,如发烧,这是一种严重的感染。在某些情况下,如果感染是由于感染引起的,可能会导致发烧。感染:感染可能会引起发热、咳嗽、喉咙痛、喉咙痛、肌肉痛、步势不畅、肿胀等症状。药物反应:一些药物可能会导致发烧,但并非所有药物都能引起发热。其他疾病:某些疾病,如气管炎、肺炎、溃疡等,也可能导致发热。因此,如果你发现自己有感染的可能性,应立即寻求医疗帮助。在医院,你可能需要去医院的医疗中心进行免疫抉择,以免引起感染。同时,保持良好的个人卫生,避免感染,也对你的身体产生负面影响。 |
可以看到,使用医疗领域知识进行过 LoRA 微调之后,LLM 在回答医疗领域相关知识的质量有了明显的提升。LoRA 微调的训练过程与 SFT 训练基本一致,不同的是需要对网络做一些调整,引入低秩矩阵,相关代码如下:
def apply_lora(model, rank=16):
for name, module in model.named_modules():
if isinstance(module, nn.Linear) and module.weight.shape[0] == module.weight.shape[1]:
lora = LoRA(module.weight.shape[0], module.weight.shape[1], rank=rank).to(model.device)
setattr(module, "lora", lora)
original_forward = module.forward
# 显式绑定
def forward_with_lora(x, layer1=original_forward, layer2=lora):
return layer1(x) + layer2(x)
module.forward = forward_with_lora
通过以上代码可以看出,对于特定的线性层,通过 hook 原来的 forward 函数,为这一层叠加了一个 LoRA 层,其实就是在原来的计算出来的 Tensor 上再加上一个 LoRA 层计算出来的 Tensor,这里要求这两个张量形状完全一样,下面是 LoRA 层的代码核心代码:
class LoRA(nn.Module):
def __init__(self, in_features, out_features, rank):
super().__init__()
self.rank = rank # LoRA的秩(rank),控制低秩矩阵的大小
self.A = nn.Linear(in_features, rank, bias=False) # 低秩矩阵A
self.B = nn.Linear(rank, out_features, bias=False) # 低秩矩阵B
# 矩阵A高斯初始化
self.A.weight.data.normal_(mean=0.0, std=0.02)
# 矩阵B全0初始化
self.B.weight.data.zero_()
def forward(self, x):
return self.B(self.A(x))
代码非常简单,两个线性层,进行了两次仿射变换,其中 rank 远小于输入大小,一般取值 4、8、16。示意图如下:
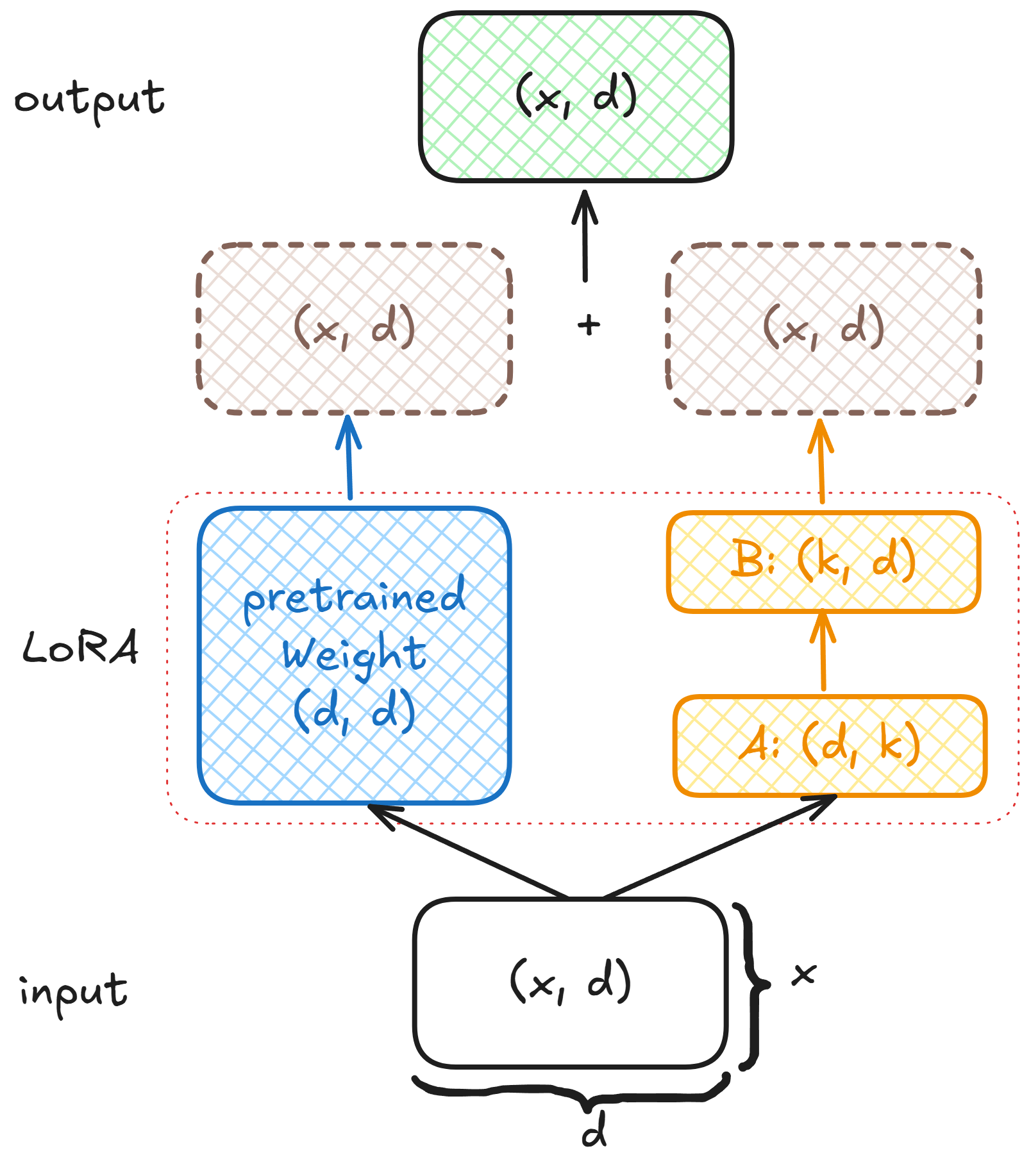
可以看出引入低秩矩阵后不影响输入输出的大小,那么引入低秩矩阵是如何减少训练参数的呢?假设原线性层大小为 (1024, 1024), 那么原线性层参数量是:1024*1024=1048576,如果 rank 取 4,则低秩矩阵A 大小为:(1024, 4),B 大小为:(4, 1024), 那么这两个矩阵参数总和是:1024*4+4*1024=8192,参数量是原来的 0.78%,通过 LoRA 微调,训练这部分比较少的参数来影响整个模型的输出。那么在训练阶段还有关键的一部就是冻结原有的权重,之训练 LoRA 层引入的相关权重,相关代码如下:
lora_params = []
for name, param in model.named_parameters():
if 'lora' not in name:
param.requires_grad = False
else:
lora_params.append(param)
# 只对 LoRA 参数进行优化
optimizer = optim.AdamW(lora_params, lr=args.learning_rate)
...
def save_lora(model, path):
state_dict = {}
for name, module in model.named_modules():
if hasattr(module, 'lora'):
lora_state = {f'{name}.lora.{k}': v for k, v in module.lora.state_dict().items()}
state_dict.update(lora_state)
torch.save(state_dict, path)
设置非 LoRA 层参数不参与梯度更新,优化器只优化 LoRA 层参数,最后,模型训练好了将 LoRA 相关权重单独保存,使用的时候再将这部分权重重新加载到 LoRA 层:
def load_lora(model, path):
state_dict = torch.load(path, map_location=model.device)
for name, module in model.named_modules():
if hasattr(module, 'lora'):
lora_state = {k.replace(f'{name}.lora.', ''): v for k, v in state_dict.items() if f'{name}.lora.' in k}
module.lora.load_state_dict(lora_state)
通过这种方式就可以加载 LoRA 训练过的模型的,但是因为加载了 LoRA 层,再推理计算的时候多了一些参数的技术,前面提到过,LoRA 的权重是可以和原模型合并的,为什么可以合并呢?
在神经网络的前向传播过程中,假设原始权重为 $\mathbf{W_0}\in\mathbb{R}^{d\times d}$,对于输入向量 $\mathbf{x}\in\mathbb{R}^{x\times d}$,使用原始权重 $\mathbf{W}$ 进行线性变换的结果为 $\mathbf{y}_{1}\in\mathbb{R}^{x\times d}$:
$$\mathbf{y}_{1}=\mathbf{x}\mathbf{W_0}$$
使用 LoRA 微调后的权重 $\mathbf{W_a}\in\mathbb{R}^{d\times k}$,$\mathbf{W_b}\in\mathbb{R}^{k\times d}$进行线性变换的结果为 $\mathbf{y}_{2}\in\mathbb{R}^{x\times d}$:
$$\mathbf{y}_{2}=\mathbf{x}\mathbf{W_a}\mathbf{W_b}$$
最后将两次计算结果相加得到最终的输出$\mathbf{y}\in\mathbb{R}^{x\times d}$:
$$\mathbf{y} = \mathbf{y_1}+\mathbf{y_2}=\mathbf{x}\mathbf{W_0}+\mathbf{x}\mathbf{W_a}\mathbf{W_b}$$
根据加法结合率:
$$\mathbf{y} = \mathbf{y_1}+\mathbf{y_2}=\mathbf{x}(\mathbf{W_0}+\mathbf{W_a}\mathbf{W_b})$$
所以有$\mathbf{W_{merged}}\in\mathbb{R}^{d\times d}$:
$$\mathbf{W_{merged}}=\mathbf{W_0}+\mathbf{W_a}\mathbf{W_b}$$
这样,在推理时只需要进行一次矩阵乘法 $\mathbf{y}=\mathbf{x}\mathbf{W_{merged}}$,而不需要分别计算 $\mathbf{x}\mathbf{W_0}$ 和 $\mathbf{x}\mathbf{W_a}\mathbf{W_b}$ 再相加,从而减少了计算量和推理时间,在推理阶段直接使用合并后的矩阵进行计算,不改变模型的计算结果,但能提高计算效率,以上就是 LoRA 微调原理分析的所有内容。实际应用中我们可以使用 transformers、peft 框架进行更方便、高效的微调。